15. Data Analysis and More Data Visualization with Python II#
Please refer to here for the data in this lecture.
Last time#
Python package: Pandas and Matplotlib
Today#
Errorbar#
Plot \(y\) versus \(x\) as lines and/or markers with attached errorbars.
Syntax
Axes.errorbar(
x, y, yerr=None, xerr=None, fmt='', ecolor=None,
elinewidth=None, capsize=None, barsabove=False,
lolims=False, uplims=False, xlolims=False, xuplims=False,
errorevery=1, capthick=None, *, data=None, **kwargs
)
import numpy as np
import matplotlib.pyplot as plt
# make data:
np.random.seed(87)
x = [3, 4, 5]
y = [9., 4., 8.7]
yerr = np.random.randn(3)
# plot:
fig = plt.figure(1, figsize=(4,3), dpi=100, layout="constrained", facecolor="w")
ax = fig.add_subplot(111)
ax.errorbar(
x,
y,
yerr,
fmt='o',
linewidth=2,
capsize=3,
)
ax.grid(True)
ax.set(
title="Example of Errorbar",
xlabel="x",
ylabel="y",
)
plt.show()
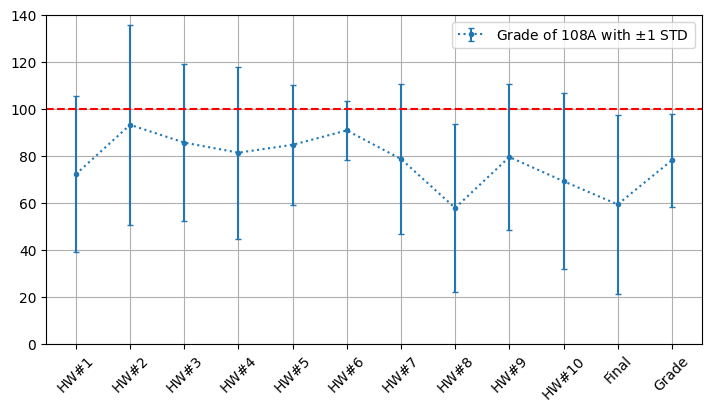
Average grade of each homework assignment#
In another universe, there is a teacher who wants to know the learning status of his students, so he wants to sort out his homework scores for each semester and try to observe some clues. In order to help him, we will need to plot the average grade of each assignment in the past years into a chart.
Calculate and plot the average grade of each homework
Use the standard deviation as the error bar of each data point
If we are lucky, we might find something.
The data is here:
Lecture15/data/data_nycudopcs.xlsx. First, let’s take a look at what it has.
import pandas as pd
data = pd.read_excel(
"./data/data_nycudopcs.xlsx",
sheet_name = None,
)
for idx, df in enumerate(data):
print(df)
print(data[df])
# print(data[df].columns)
print("="*100)
108A
item HW#1 HW#2 HW#3 HW#4 HW#5 HW#6 \
0 mean 72.129032 93.161290 85.580645 81.290323 84.645161 90.774194
1 std 33.206166 42.563754 33.557686 36.577947 25.508885 12.637800
HW#7 HW#8 HW#9 HW#10 Final Grade
0 78.612903 57.741935 79.451613 69.129032 59.245161 78.064516
1 32.023614 35.719246 31.258960 37.397631 38.194026 19.753372
====================================================================================================
111A
item HW#1 HW#2 HW#3 HW#4 HW#5 HW#6 \
0 mean 83.613636 83.340909 87.613636 79.568182 80.931818 90.340909
1 std 21.750398 31.591832 20.517963 13.855396 25.082559 25.911247
HW#7 HW#8 HW#9 HW#10 Final Grade
0 77.250000 101.522727 98.227273 96.750000 61.325758 84.894848
1 12.970674 29.941407 55.223379 37.473169 32.289988 15.606122
====================================================================================================
112A
item HW#1 HW#2 HW#3 HW#4 HW#5 HW#6 \
0 mean 87.209302 78.837209 78.372093 78.372093 52.325581 62.093023
1 std 32.317295 26.543702 27.618165 27.253679 43.470691 41.017310
HW#7 HW#8 HW#9 HW#10 Final Grade
0 89.302326 128.255814 50.000000 107.906977 66.364341 80.646512
1 18.308903 37.319147 43.588989 50.097911 30.683727 19.716038
====================================================================================================
Plot the data of 108A#
Once we know what the material has, we can choose a specific semester to plot.
# Plot the data of 108A
data_108 = pd.read_excel("./data/data_nycudopcs.xlsx", sheet_name="108A")
x = np.arange(len(data_108.columns[1:]))
fig = plt.figure(1, figsize=(7,4), dpi=100, layout="constrained", facecolor="w")
ax = fig.add_subplot(111)
ax.errorbar(
x = x,
y = data_108.iloc[0][1:],
yerr = data_108.iloc[1][1:],
label = r"Grade of 108A with $\pm 1$ STD",
capsize = 2,
marker = ".",
linestyle = "dotted",
)
xmin, xmax = ax.get_xlim()
ax.hlines(
y = [100],
xmin = xmin,
xmax = xmax,
colors = "r",
linestyles = "dashed",
)
ax.set_xlim([xmin, xmax])
ax.set_ylim([0, 140])
ax.set_xticks(x)
ax.set_xticklabels(
data_108.columns[1:],
fontdict={
'horizontalalignment': 'center',
"rotation": 45,
}
)
ax.legend(loc="best")
ax.grid(True)
plt.show()
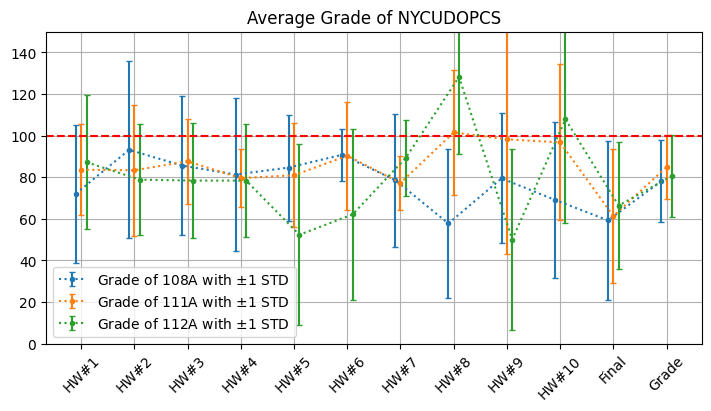
Plot all#
It would be more convenient if we plot all the data.
We can write a function to iteratively plot the data.
def plotGrade(data):
fig = plt.figure(1, figsize=(7,4), dpi=100, layout="constrained", facecolor="w")
ax = fig.add_subplot(111)
for idx, df in enumerate(data):
currentDF = data[df]
x = np.arange(len(currentDF.columns[1:]))
ax.errorbar(
x = x + 0.1*(idx-1),
y = currentDF.iloc[0][1:],
yerr = currentDF.iloc[1][1:],
label = "Grade of {} with ".format(df) + r"$\pm 1$ STD",
capsize = 2,
marker = ".",
linestyle = "dotted",
)
xmin, xmax = ax.get_xlim()
ax.hlines(
y = [100],
xmin = xmin,
xmax = xmax,
colors = "r",
linestyles = "dashed",
)
ax.set(
xlim=(xmin, xmax),
ylim=(0, 150),
xticks=x,
title="Average Grade of NYCUDOPCS",
)
ax.set_xticklabels(
currentDF.columns[1:],
fontdict={
'horizontalalignment': 'center',
"rotation": 45,
}
)
ax.legend(loc="best")
ax.grid(True)
plt.show()
data = pd.read_excel(
"./data/data_nycudopcs.xlsx",
sheet_name = None,
)
plotGrade(data)
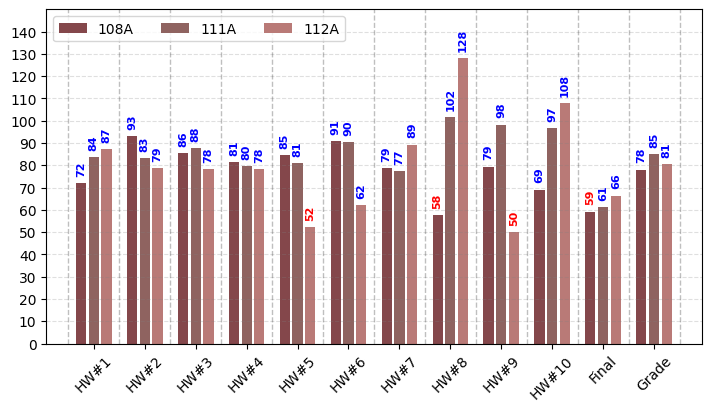
Bar plot#
Vertical bar plot#
Make a bar plot.
Syntax
Axes.bar(
x, height, width=0.8, bottom=None, *,
align='center', data=None, **kwargs
)
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
def plotBarV(data):
colors = ("#84474B", "#8F6360", "#B97A77", "#DFCFCC")
fig = plt.figure(1, figsize=(7,4), dpi=100, layout="constrained", facecolor="w")
ax = fig.add_subplot(111)
for idx, df in enumerate(data):
currentDF = data[df]
x = np.arange(len(currentDF.columns[1:]))
rects = ax.bar(
x=x + 0.25*(idx-1),
width=0.2,
align="center",
height=currentDF.iloc[0][1:],
color=colors[idx],
label="{}".format(df),
)
large_bars = ["{:.0f}".format(v) if v > 60 else '' for v in currentDF.iloc[0][1:]]
small_bars = ["{:.0f}".format(v) if v <= 60 else '' for v in currentDF.iloc[0][1:]]
ax.bar_label(
container=rects,
labels=large_bars,
padding=5,
color='b',
fontweight='bold',
fontsize=8,
rotation=90,
)
ax.bar_label(
container=rects,
labels=small_bars,
padding=5,
color='r',
fontweight='bold',
fontsize=8,
rotation=90,
)
xmin, xmax = ax.get_xlim()
ax.set(
xlim=(xmin, xmax),
xticks=x,
ylim=(0, 150),
yticks=np.arange(0, 150, 10),
)
ax.set_xticklabels(
currentDF.columns[1:],
fontdict={
'horizontalalignment': 'center',
"rotation": 45,
}
)
ax.yaxis.grid(True, linestyle='--', which='major', color='grey', alpha=.25)
ax.vlines(np.arange(-.5, 12, 1), ymin=0, ymax=150, colors="k", alpha=.25, linestyle='--', linewidth=1)
# ax.axhline(60, color='r', alpha=0.25)
ax.legend(loc="upper left", ncols=3)
plt.show()
plotBarV(data)
Horizontal bar plot#
Make a horizontal bar plot..
Syntax
Axes.barh(
y, width, height=0.8, left=None, *,
align='center', data=None, **kwargs
)
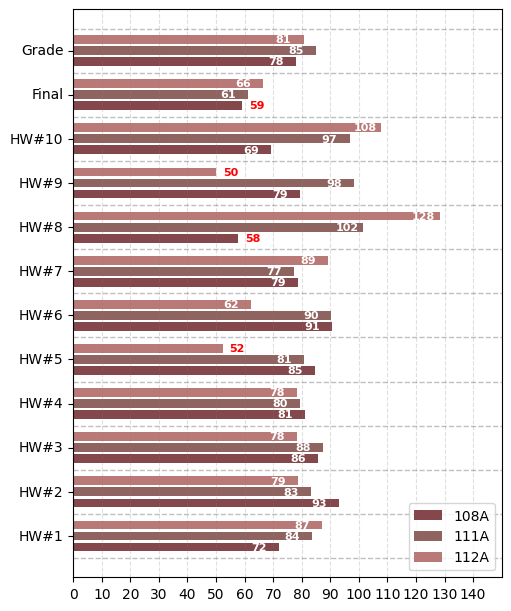
Exercise 15.1#
Please transform the above vertical bar plot into horizontal bar plot like this image.
3D plotting#
Plot 2D data on 3D plot#
First, we have to create a 3D figure (a
Axes3Dobject) viaprojection.Syntax
Axes3D.plot(xs, ys, *args, zdir='z', **kwargs)
# How to create?
ax3d = matplotlib.pyplot.figure().add_subplot(projection='3d')
import matplotlib.pyplot as plt
import numpy as np
x = np.linspace(0, 1, 100)
y = np.sin(2 * np.pi * x)
np.random.seed(19890604)
x2 = np.random.sample(64)
y2 = np.random.sample(64)
fig = plt.figure(figsize=(10,4), dpi=100)
# Create a 2D plot
ax1 = fig.add_subplot(121)
ax1.plot(x, y, label=r"sin(2$\pi$x)")
ax1.scatter(x2, y2, c="r", marker="^")
ax1.set(
xlim=(0, 1),
ylim=(-1,1),
xlabel=r"$x$",
ylabel=r"$y$",
)
ax1.legend()
# Create a 3D plot
ax2 = fig.add_subplot(122, projection='3d')
# zs=0, zdir='z'
ax2.plot(xs=x, ys=y, zs=0, zdir='z', color="b", label=r'y = sin(2$\pi$x)')
# zs=0.5, zdir='z'
ax2.plot(xs=x, ys=y, zs=0.5, zdir='z', color="g", label=r"y = sin(2$\pi$x)")
# zs=0, zdir='y'
ax2.plot(xs=x, ys=y, zs=0, zdir='y', color="r", label=r"y = sin(2$\pi$x)")
# zs=0, zdir='x'
ax2.plot(xs=x, ys=y, zs=0, zdir='x', color="k", label=r"y = sin(2$\pi$x)")
ax2.set(
xlim=(0, 1),
ylim=(-1,1),
zlim=(0, 1),
xlabel=r"$x$",
ylabel=r"$y$",
zlabel=r"$z$",
)
ax2.legend()
ax2.view_init(elev=30, azim=30, roll=0)
plt.show()
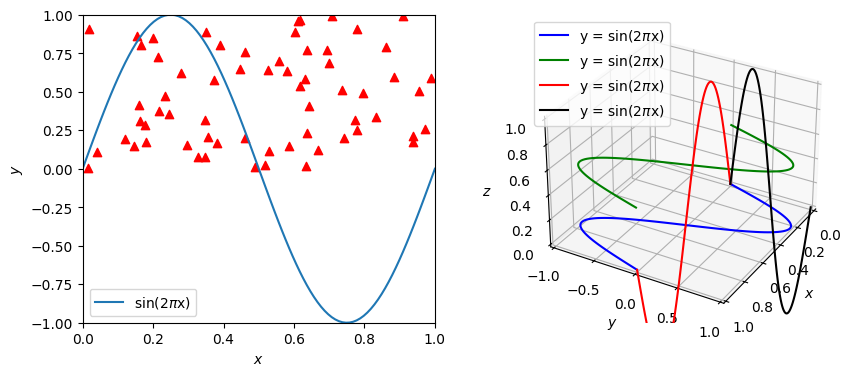
Exercise 15.2#
In our previouse 3D plot, we didn’t plot the scatters shown in the left subplot. Please plot those scatters in your 3D plot.
You may want to try different parameters (
zsandzdir).
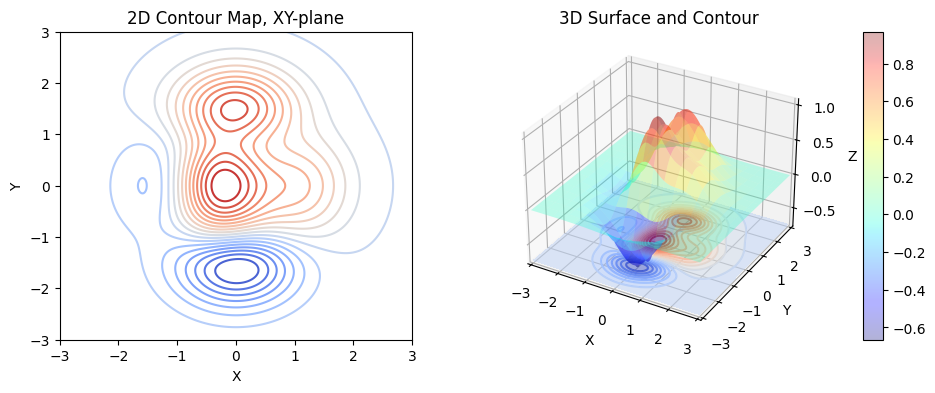
Plot a surface and contours on 3D plot#
We have learned how to plot 2D contours. It is time to learn how to plot a 3D surface and its corresponding projection on a 3D plot.
Syntax
Axes3D.plot_surface(
X, Y, Z, *, norm=None,
vmin=None, vmax=None, lightsource=None, **kwargs
)
For example, to plot the surface of function \(f(x,y)\) in the region \(x \in [-3, 3]\) and \(y \in [-3, 3]\):
import matplotlib.pyplot as plt
import numpy as np
import matplotlib.transforms as mtransforms
def add_right_cax(ax, pad, width):
axpos = ax.get_position()
caxpos = mtransforms.Bbox.from_extents(
axpos.x1 + pad,
axpos.y0,
axpos.x1 + pad + width,
axpos.y1,
)
cax = ax.figure.add_axes(caxpos)
return cax
# Prepare the data
L = 3
x = np.linspace(-L, L, 501) # Create a 1D array, shape: (501,)
y = np.linspace(-L, L, 501) # Create a 1D array, shape: (501,)
X, Y = np.meshgrid(x, y) # Create two 2D arrays, shape: (501, 501)
Z = (1 - X/2 + X**3 + Y**5) * np.exp(-(X**2 + Y**2)) # Create a 2D array Z = f(X, Y)
lv = np.linspace(np.min(Z), np.max(Z), 20)
fig = plt.figure(figsize=(10,4), dpi=100)
ax1 = fig.add_subplot(121)
ax1.contour(X, Y, Z, levels=lv, cmap='coolwarm')
ax1.set(
xlim=(-L, L),
ylim=(-L, L),
xlabel="X",
ylabel="Y",
title="2D Contour Map, XY-plane",
)
ax2 = fig.add_subplot(122, projection='3d')
# Plot the 3D surface
surf = ax2.plot_surface(
X, Y, Z,
cmap="jet",
# edgecolor='royalblue', # linecolor
lw=0.5, # linewidth
rstride=32,
cstride=32,
alpha=0.3,
)
cax2 = add_right_cax(ax=ax2, pad=0.05, width=0.02)
cbar2 = fig.colorbar(mappable=surf, cax=cax2)
# Plot the 2D contours on 3D plot
ax2.contour(X, Y, Z, zdir='z', stride=32, offset=np.min(Z), cmap='coolwarm', levels=lv)
ax2.contourf(X, Y, Z, zdir='z', offset=np.min(Z), cmap='coolwarm', levels=lv, alpha=0.5)
ax2.set(
xlim=(-L, L),
ylim=(-L, L),
zlim=(np.min(Z), np.max(Z)),
xlabel='X',
ylabel='Y',
zlabel='Z',
title="3D Surface and Contour",
)
plt.show()
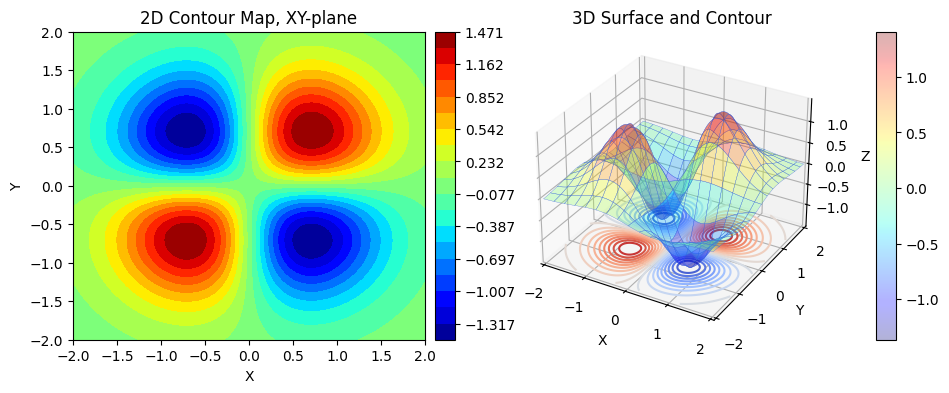
Exercise 15.3#
Please plot the surface of function \(f(x,y)\):
Pie charts#
Plot a pie chart.
Syntax
Axes.pie(
x, explode=None, labels=None, colors=None, autopct=None, pctdistance=0.6,
shadow=False, labeldistance=1.1, startangle=0, radius=1, counterclock=True,
wedgeprops=None, textprops=None, center=(0, 0), frame=False, rotatelabels=False,
*, normalize=True, hatch=None, data=None
)
import matplotlib.pyplot as plt
labels = ['Cats', 'Lions', 'Leopards', 'Tigers']
sizes = [15, 30, 45, 10]
fig = plt.figure(figsize=(12,4), dpi=100)
ax1 = fig.add_subplot(131)
ax1.pie(
x=sizes,
labels=labels
)
# Add the percent size in wedge
ax2 = fig.add_subplot(132)
ax2.pie(
x=sizes,
labels=labels,
autopct=lambda s: "{:.1f}%".format(s),
pctdistance=0.6,
labeldistance=1.1,
)
# Swap the percentage and wedge labels
ax3 = fig.add_subplot(133)
ax3.pie(
x=sizes,
labels=labels,
autopct=lambda s: "{:.1f}%".format(s),
pctdistance=1.2,
labeldistance=0.4,
)
plt.show()
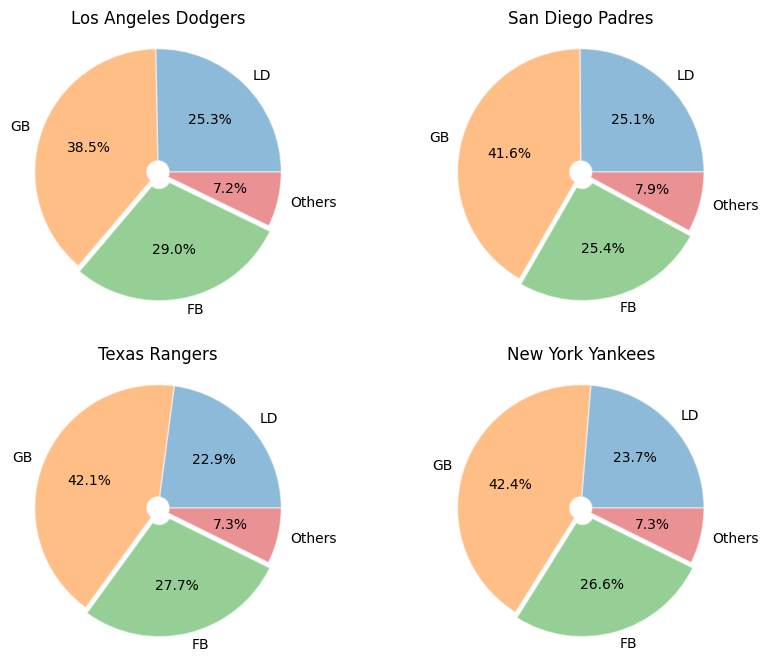
The batted ball of MLB#
In a baseball game, there are several situations when a batter hit a ball in play, including line drive (LD), ground ball (GB), fly ball (FB), pop-up (PU), safety bunt, sacrifice fly (SF), and others (the ball hit a umpire, …).
Typically, baseball statistics use three percentages, the line drive percentage (LD%), the ground ball percentage (GB%), and the fly ball percentage (FB%), to evaluate the basic batting statistica of a player or a team.
In this example, we would like to plot a pie chart to summarize this.
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
data = pd.read_csv("./data/data_batting2024_team.csv")
teamList = [
"Los Angeles Dodgers",
"San Diego Padres",
"Texas Rangers",
"New York Yankees",
]
labels = ['LD', 'GB', 'FB', 'Others']
explode = (0, 0, 0.05, 0)
fig = plt.figure(figsize=(10, 8), dpi=100)
for idx, team in enumerate(teamList):
currentData = data[data["Tm"] == team]
# Get LD%, GB%, FB% and transfer to float
battedBall = [
float(currentData["LD%"].to_list().pop().split(sep="%")[0]), # LD%
float(currentData["GB%"].to_list().pop().split(sep="%")[0]), # GB%
float(currentData["FB%"].to_list().pop().split(sep="%")[0]), # FB%
]
# Calculate the others
battedBall.append(100 - sum(battedBall))
ax = fig.add_subplot(2, 2, idx+1)
ax.pie(
x=battedBall,
labels=labels,
explode=explode,
# shadow=True,
radius=1.1,
autopct=lambda s: "{:.1f}%".format(s),
pctdistance=0.6,
labeldistance=1.1,
wedgeprops={
"linewidth": 1,
"edgecolor": "white",
"alpha": 0.5,
"width": 1.,
},
)
ax.set_title(team)
plt.show()
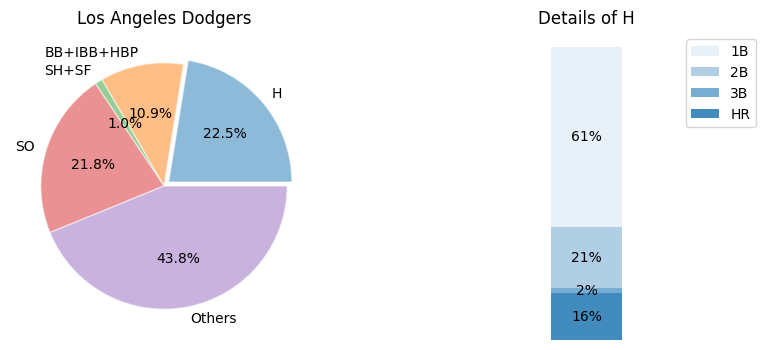
Pie charts with bar#
Sometimes, we would like to further investigate one of the wedges of a pie chart. In this case, we can use a bar plot to demonstrate its characteristics.
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
data = pd.read_csv("./data/data_batting2024_team.csv")
team = "Los Angeles Dodgers"
labels = ["H", "BB+IBB+HBP", "SH+SF", "SO", "Others"]
explode = (0.05, 0, 0, 0, 0)
fig = plt.figure(figsize=(10, 4), dpi=100)
currentData = data[data["Tm"] == team]
# Get H, BB+IBB+HBP, SH+SF, and SO
battedBall = [
currentData["H"].to_numpy()[0], # H
currentData["BB"].to_numpy()[0] + currentData["IBB"].to_numpy()[0] + currentData["HBP"].to_numpy()[0], # BB+IBB+HBP
currentData["SH"].to_numpy()[0] + currentData["SF"].to_numpy()[0], # SH+SF
currentData["SO"].to_numpy()[0], # SO
]
# Calculate the others
battedBall.append(currentData["PA"].to_numpy()[0] - sum(battedBall))
# Pie chart
ax = fig.add_subplot(1, 2, 1)
ax.pie(
x=battedBall,
labels=labels,
explode=explode,
startangle=0,
autopct=lambda s: "{:.1f}%".format(s),
pctdistance=0.6,
labeldistance=1.1,
wedgeprops={
"linewidth": 1,
"edgecolor": "white",
"alpha": 0.5,
},
)
ax.set_title(team)
# Get 1B, 2B, 3B, and HR
hList = [
currentData["2B"].to_numpy()[0],
currentData["3B"].to_numpy()[0],
currentData["HR"].to_numpy()[0],
]
hList.insert(0, currentData["H"].to_numpy()[0] - sum(hList))
hList = hList/currentData["H"].to_numpy()[0]
hLabels = ['1B', '2B', '3B', 'HR']
bottom = 1
width = .2
# Bar plot
ax2 = fig.add_subplot(1, 2, 2)
for j, (height, label) in enumerate(zip(hList, hLabels)):
bottom -= height
bc = ax2.bar(
0,
height,
width,
bottom=bottom,
color='C0',
label=label,
alpha=0.1 + 0.25 * j,
)
ax2.bar_label(
bc,
labels=["{:.0%}".format(height)],
label_type='center',
)
ax2.set_title('Details of H')
ax2.legend()
ax2.axis('off')
ax2.set_xlim(- 2.5 * width, 2.5 * width)
plt.show()
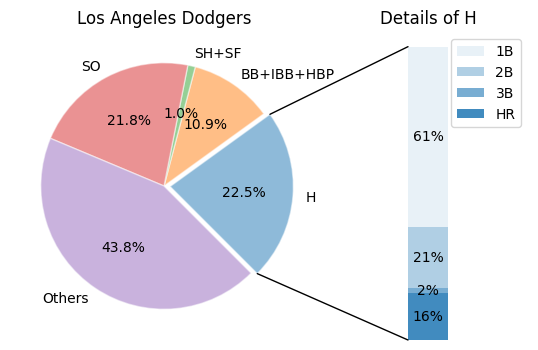
Add bar via matplotlib.transforms#
To further control the position of bar (or other sub-figures), the
matplotlib.transformscan provide a more compact result.
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import matplotlib.transforms as mtransforms
from matplotlib.patches import ConnectionPatch
def add_right_ax(ax, pad, width):
axpos = ax.get_position()
caxpos = mtransforms.Bbox.from_extents(
axpos.x1 + pad,
axpos.y0,
axpos.x1 + pad + width,
axpos.y1,
)
right_ax = ax.figure.add_axes(caxpos)
return right_ax
data = pd.read_csv("./data/data_batting2024_team.csv")
team = "Los Angeles Dodgers"
labels = ["H", "BB+IBB+HBP", "SH+SF", "SO", "Others"]
explode = (0.05, 0, 0, 0, 0)
fig = plt.figure(figsize=(10, 4), dpi=100)
currentData = data[data["Tm"] == team]
# Get H, BB+IBB+HBP, SH+SF, and SO
battedBall = [
currentData["H"].to_numpy()[0], # H
currentData["BB"].to_numpy()[0] + currentData["IBB"].to_numpy()[0] + currentData["HBP"].to_numpy()[0], # BB+IBB+HBP
currentData["SH"].to_numpy()[0] + currentData["SF"].to_numpy()[0], # SH+SF
currentData["SO"].to_numpy()[0], # SO
]
# Calculate the others
battedBall.append(currentData["PA"].to_numpy()[0] - sum(battedBall))
# Pie chart
ax1 = fig.add_subplot(1, 2, 1)
wedges, *_ = ax1.pie(
x=battedBall,
labels=labels,
explode=explode,
startangle=-45,
autopct=lambda s: "{:.1f}%".format(s),
pctdistance=0.6,
labeldistance=1.1,
wedgeprops={
"linewidth": 1,
"edgecolor": "white",
"alpha": 0.5,
},
)
ax1.set_title(team)
# Get 1B, 2B, 3B, and HR
hList = [
currentData["2B"].to_numpy()[0],
currentData["3B"].to_numpy()[0],
currentData["HR"].to_numpy()[0],
]
hList.insert(0, currentData["H"].to_numpy()[0] - sum(hList))
hList = hList/currentData["H"].to_numpy()[0]
hLabels = ['1B', '2B', '3B', 'HR']
bottom = 1
width = .2
ax2 = add_right_ax(ax=ax1, pad=0.01, width=0.2)
# Bar plot
for j, (height, label) in enumerate(zip(hList, hLabels)):
bottom -= height
bc = ax2.bar(
0,
height,
width,
bottom=bottom,
color='C0',
label=label,
alpha=0.1 + 0.25 * j,
)
ax2.bar_label(
bc,
labels=["{:.0%}".format(height)],
label_type='center',
)
ax2.set_title('Details of H')
ax2.legend()
ax2.axis('off')
ax2.set_xlim(- 2.5 * width, 2.5 * width)
# use ConnectionPatch to draw lines between the two plots
theta1, theta2 = wedges[0].theta1, wedges[0].theta2
center, r = wedges[0].center, wedges[0].r
bar_height = sum(hList)
# draw top connecting line
x = r * np.cos(np.pi / 180 * theta2) + center[0]
y = r * np.sin(np.pi / 180 * theta2) + center[1]
con = ConnectionPatch(xyA=(-width / 2, bar_height), coordsA=ax2.transData,
xyB=(x, y), coordsB=ax1.transData)
con.set_color([0, 0, 0])
con.set_linewidth(1)
ax2.add_artist(con)
# draw bottom connecting line
x = r * np.cos(np.pi / 180 * theta1) + center[0]
y = r * np.sin(np.pi / 180 * theta1) + center[1]
con = ConnectionPatch(xyA=(-width / 2, 0), coordsA=ax2.transData,
xyB=(x, y), coordsB=ax1.transData)
con.set_color([0, 0, 0])
con.set_linewidth(1)
ax2.add_artist(con)
plt.show()
Reference#
The data of this lecture is from Baseball Reference.
Don't click this
Exercise 15.1
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
def plotBarH(data):
colors = ("#84474B", "#8F6360", "#B97A77", "#DFCFCC")
fig = plt.figure(1, figsize=(5,6), dpi=100, layout="constrained", facecolor="w")
ax = fig.add_subplot(111)
for idx, df in enumerate(data):
currentDF = data[df]
x = np.arange(len(currentDF.columns[1:]))
rects = ax.barh(
y=x + 0.25*(idx-1),
width=currentDF.iloc[0][1:],
align="center",
height=0.2,
color=colors[idx],
label="{}".format(df),
)
large_bars = ["{:.0f}".format(v) if v > 60 else '' for v in currentDF.iloc[0][1:]]
small_bars = ["{:.0f}".format(v) if v <= 60 else '' for v in currentDF.iloc[0][1:]]
ax.bar_label(
container=rects,
labels=large_bars,
padding=-20,
color='w',
fontweight='bold',
fontsize=8,
)
ax.bar_label(
container=rects,
labels=small_bars,
padding=5,
color='r',
fontweight='bold',
fontsize=8,
)
ymin, ymax = ax.get_ylim()
ax.set(
xlim=(0, 150),
xticks=np.arange(0, 150, 10),
ylim=(ymin, ymax),
yticks=x,
)
ax.set_yticklabels(
currentDF.columns[1:],
fontdict={
'verticalalignment': 'center',
"rotation": 0,
}
)
ax.xaxis.grid(True, linestyle='--', which='major', color='grey', alpha=.25)
ax.hlines(np.arange(-.5, 12, 1), xmin=0, xmax=150, colors="k", alpha=.25, linestyle='--', linewidth=1)
ax.legend(loc="lower right", ncols=1)
plt.show()
data = pd.read_excel(
"./data/data_nycudopcs.xlsx",
sheet_name = None,
)
plotBarH(data)
Exercise 15.3
import matplotlib.pyplot as plt
import numpy as np
L = 2
x = np.linspace(-L, L, 501) # Create a 1D array, shape: (501,)
y = np.linspace(-L, L, 501) # Create a 1D array, shape: (501,)
X, Y = np.meshgrid(x, y) # Create two 2D arrays, shape: (501, 501)
Z = 8 * X * Y * np.exp(-(X**2 + Y**2))
lv = np.linspace(np.min(Z), np.max(Z), 20)
fig = plt.figure(figsize=(10,4), dpi=100)
ax1 = fig.add_subplot(121)
im1 = ax1.contourf(X, Y, Z, levels=lv, cmap='jet')
ax1.set(
xlim=(-L, L),
ylim=(-L, L),
xlabel="X",
ylabel="Y",
title="2D Contour Map, XY-plane",
)
cax1 = add_right_cax(ax=ax1, pad=0.01, width=0.02)
cbar1 = fig.colorbar(mappable=im1, cax=cax1)
ax2 = fig.add_subplot(122, projection='3d')
# Plot the 3D surface
surf = ax2.plot_surface(
X, Y, Z,
edgecolor='royalblue',
cmap="jet",
lw=0.2,
rstride=32,
cstride=32,
alpha=0.3,
)
ax2.contour(X, Y, Z, zdir='z', stride=32, offset=np.min(Z), cmap='coolwarm', levels=lv)
# ax2.contourf(X, Y, Z, zdir='x', offset=-L, cmap='jet', levels=lv)
# ax2.contourf(X, Y, Z, zdir='y', offset=L, cmap='jet', levels=lv)
ax2.set(
xlim=(-L, L),
ylim=(-L, L),
zlim=(np.min(Z), np.max(Z)),
xlabel='X',
ylabel='Y',
zlabel='Z',
title="3D Surface and Contour",
)
cax2 = add_right_cax(ax=ax2, pad=0.05, width=0.02)
cbar2 = fig.colorbar(mappable=surf, cax=cax2)
plt.show()
