03. Simple Numerical Algorithms I#
Last time#
Introduction to Python
String
Logistic operators
Branching and conditionals
Iterations and loops
Today#
Exhaustive enumeration#
The fundamental of algorithms
Start with a guess
Check if the guess is the solution
If not, keep guessing until you get the solution
Example: finding the square root of a perfect square number \(x\)
Start with a guess \(g\)
If \(g \times g\) is close enough to \(x\), stop and say that \(g\) is the answer
Otherwise create a new guess \(g = g + 1\)
Repeat the process until close enough
# Find the square root of a perfect square number
x = 121
# Start with a guess
g = 0
while g**2 < x:
g += 1
# Check the result
if g**2 != x:
print(x, "is not a perfect square number.")
else:
print("The square root of {} is {}.".format(x, g))
The square root of 121 is 11.
Exercise 3.1#
Finding the cube root of a perfect cube \(x\)
Here is your instruction:
Start with a guess \(g\)
If \(g^3\) is close enough to \(x\), stop and say that \(g\) is the answer
Otherwise create a new guess \(g = g + 1\)
Repeat the process until close enough
Try these two numbers:
781,229,961
853,860,064,303
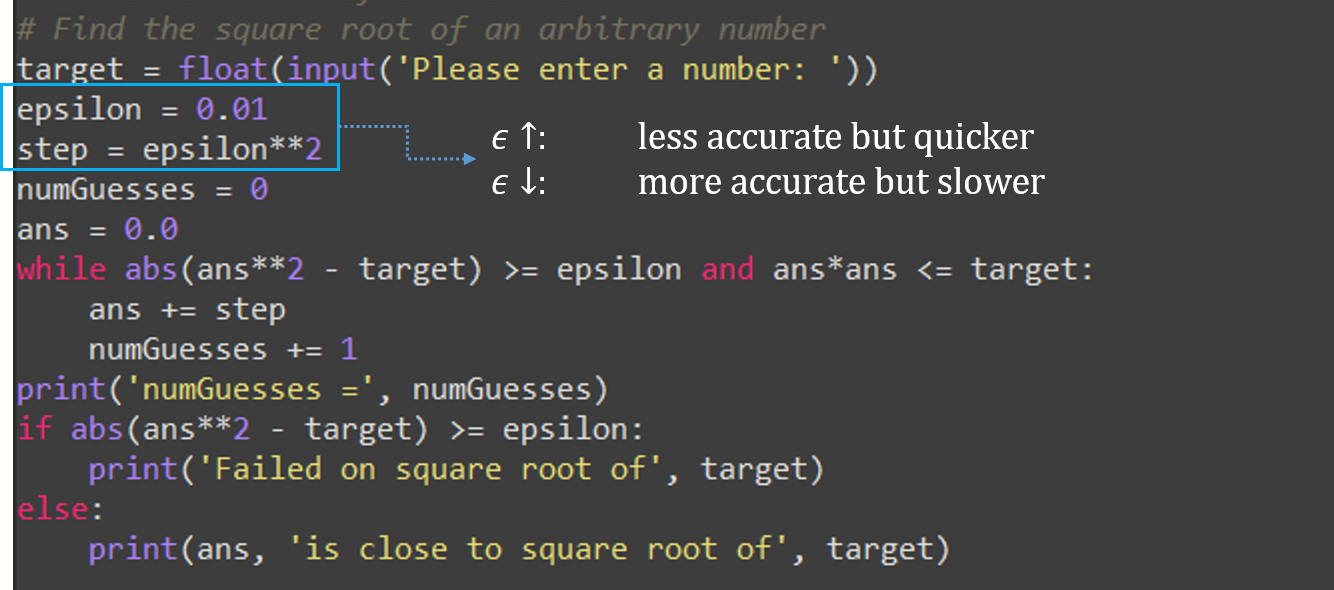
Approximation#
Aims to find a “good enough” solution
Start with a guess \(g\)
Define an acceptable minimum deviation \(\epsilon\)
Check if the guess is “close enough” to solution
Otherwise create a new guess by \(g = g + \epsilon^2\)
Repeat the process until close enough
# Find the square root of an arbitrary number
x = 121.
# Start with a guess
g = 0.0
# Define minimum deviation
epsilon = 0.01
# Step
step = epsilon**2
numGuesses = 0
while abs(g**2 - x) >= epsilon and g <= x:
g += step
numGuesses += 1
# Check the result
if abs(g**2 - x) >= epsilon:
print("Failed on finding the square root of {:.2f}".format(x))
else:
print("{:.4f} is close to the square root of {:.2f}".format(g, x))
# How many steps do we have?
print("# of guesses = {}".format(numGuesses))
10.9996 is close to the square root of 121.00
# of guesses = 109996
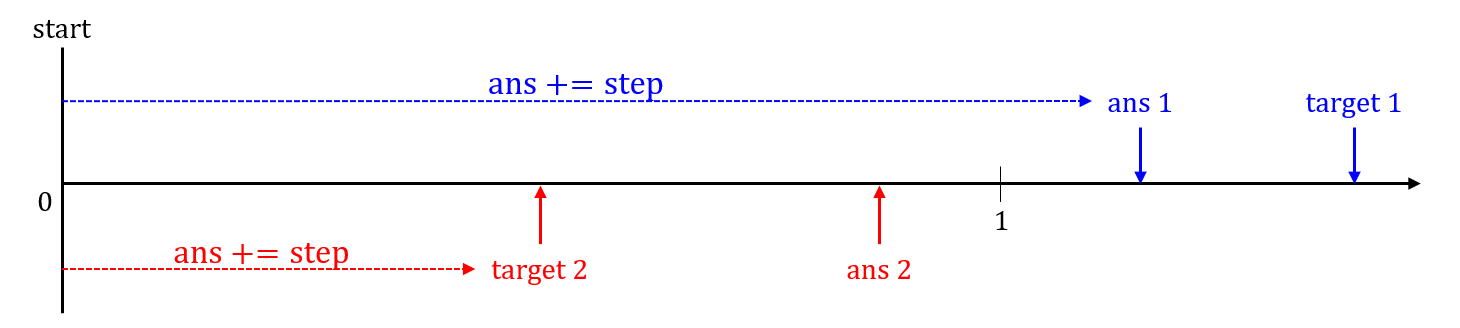
The blindside of exhaustive enumeration#
Exhaustive enumeration only works when the set of value being searched includes the answer
Try any number less than 1, e.g. 0.04
The concept of computational complexity#
How many guesses do our program need to find an approximated solution?
Find a root of an equation#
Previous examples have shown as how to find an approximated squared or cubic root. This is equivalent to find a root of an equation:
Therefore, we can numerically “solve” an equation via the same technique. For example, we want to solve this:
We just need to follow the same procedure.
Start with a guess \(g\)
Define an acceptable minimum deviation \(\epsilon\)
Check if the guess is “close enough” to solution
Otherwise create a new guess by \(g = g + \epsilon^2\)
Repeat the process until close enough
# Find the root of an equation
# Create a function object
f = lambda x: 2*x**3 - 11*x**2 + 2*x + 15
# Start with a guess
g = 0.0
# Define minimum deviation
epsilon = 0.1
# Step
step = epsilon**2
numGuesses = 0
while abs(f(g) - 0) >= epsilon:
g += step
numGuesses += 1
# Check the result
if abs(f(g) - 0) >= epsilon:
print("Failed on finding the root.")
else:
print("Find an approximated root: {:.04f}".format(g))
# How many steps do we have?
print("# of guesses = {}".format(numGuesses))
Find an approximated root: 1.5000
# of guesses = 150
A small function object: lambda#
A lambda function is a small anonymous function.
A lambda function can take any number of arguments, but can only have one expression.
# Syntax
a = lambda arguments: expression
# Examples
# 1
f = lambda x: 2*x**3 - 11*x**2 + 2*x + 15
# 2
a = lambda x, y: (x + y) * (x - y)
More details about the function object will be introduced in the next lecture.
# Examples
# 1
f = lambda x: 2*x**3 - 11*x**2 + 2*x + 15
for i in range(5):
print("f({}) = {}".format(i, f(i)))
print("="*20)
# 2
a = lambda x, y: (x + y) * (x - y)
for i in range(5):
x = i**2
y = i-1
print("a({}, {}) = {}".format(x, y, a(x, y)))
f(0) = 15
f(1) = 8
f(2) = -9
f(3) = -24
f(4) = -25
====================
a(0, -1) = -1
a(1, 0) = 1
a(4, 1) = 15
a(9, 2) = 77
a(16, 3) = 247
Exercise 3.2#
We have already found a root of equation \(2x^3 - 11x^2 + 2x + 15 = 0\).
However, our mathematical intuition tells us there are more roots for a cubic equation. Please find an another root of this equation.
Hint: try to find a root along \(x<0\).
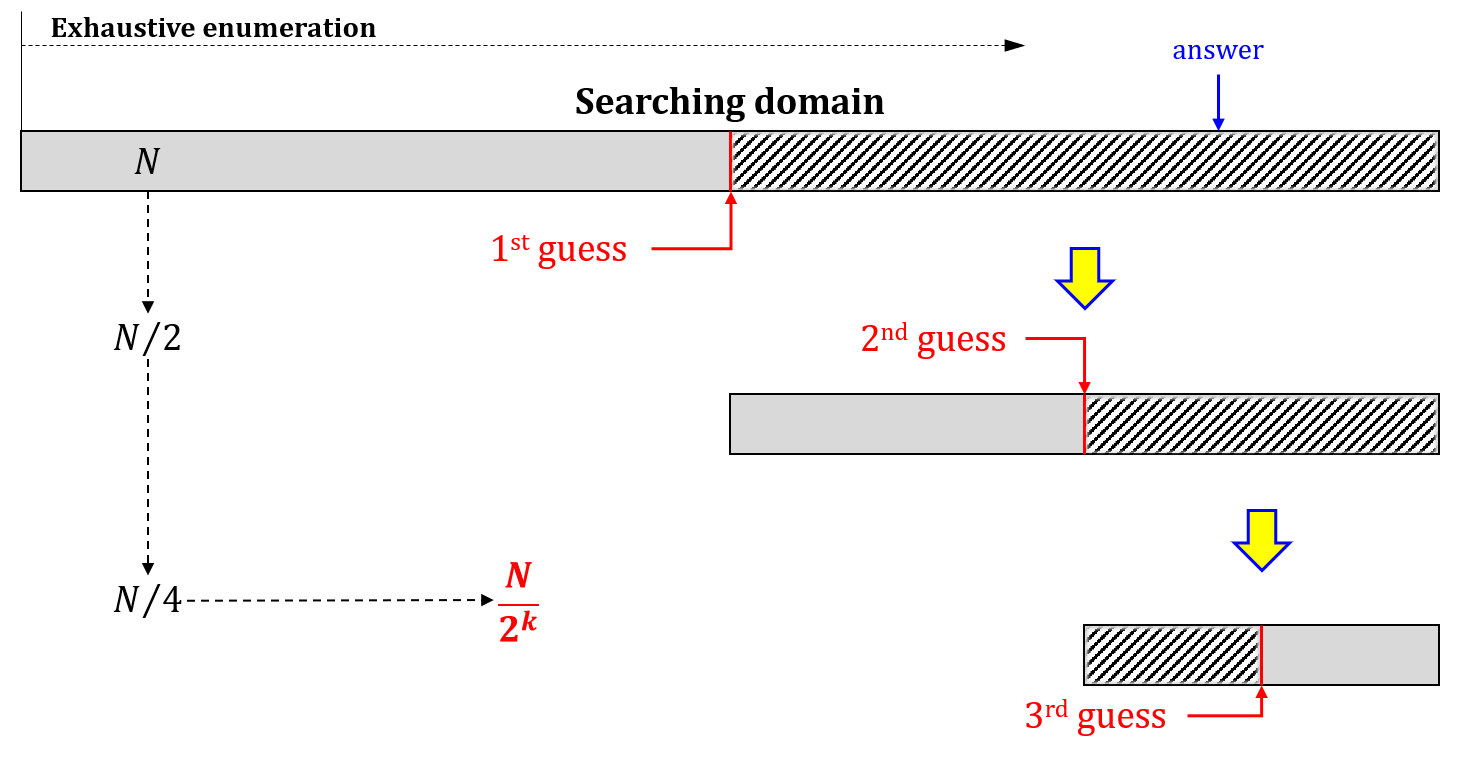
Bisection search#
Divide the searching domain into half after each iteration
An efficient way to search the answer
# Example of bisection search
x = 0.04
# Define minimum deviation
epsilon = 0.01
# Set searching region
lower_bnd = 0.0
upper_bnd = max(1., x)
# Start with a guess
g = (upper_bnd + lower_bnd)/2
numGuesses = 0
while abs(g**2 - x) >= epsilon:
print("Current search region: [{:.4f}, {:.4f}]".format(lower_bnd, upper_bnd))
numGuesses += 1
# bisection search
if g**2 < x:
lower_bnd = g
else:
upper_bnd = g
# define a new searching region
g = (upper_bnd + lower_bnd)/2
# Check the result
if abs(g**2 - x) >= epsilon:
print("Failed on finding the square root of {:.2f}".format(x))
else:
print("{:.4f} is close to the square root of {:.2f}".format(g, x))
# How many steps do we have?
print("# of guesses = {}".format(numGuesses))
Current search region: [0.0000, 1.0000]
Current search region: [0.0000, 0.5000]
Current search region: [0.0000, 0.2500]
0.1875 is close to the square root of 0.04
# of guesses = 3
Find a root of an equation via bisection search#
Again, we can numerically solve an equantion via bisection search. For example, find a root of this equation:
To achieve this, we have to understand a theorem called the intermediate value theorem.
Consider an interval \(\displaystyle I=[a,b]\) of real numbers \(\mathbb{R}\) and a continuous function \({\displaystyle f\colon I\to \mathbb {R} }\). Then
Version 1: if \(u\) is a number between \(f(a)\) and \(f(b)\), that is, \(\min(f(a),f(b))<u<\max(f(a),f(b)),\) then there is a \(c\in (a,b)\) such that \(f(c)=u\).
Version 2: the image set \(f(I)\) is also a closed interval, and it contains \({\bigl [}\min(f(a),f(b)),\max(f(a),f(b)){\bigr ]}\)
# Find the root of an equation via bisection search
# Create a function object
f = lambda x: x**2 - 2*x - 2
# Define minimum deviation
epsilon = 0.01
# Set searching region
lower_bnd = 0.
upper_bnd = 10.
# Check boundary state
lowerState = True if f(lower_bnd) > 0 else False
upperState = True if f(upper_bnd) > 0 else False
# Start with a guess
g = (upper_bnd + lower_bnd)/2
numGuesses = 0
while abs(f(g) - 0) >= epsilon:
print("Current search region: [{:.4f}, {:.4f}]".format(lower_bnd, upper_bnd))
numGuesses += 1
currentState = True if f(g) > 0 else False
print(" Current guess = {:.04f}".format(g))
print(" (lower, current, upper) = ({}, {}, {})".format(lowerState, currentState, upperState))
# bisection search
if currentState == lowerState:
lower_bnd = g
else:
upper_bnd = g
# define a new searching region
g = (upper_bnd + lower_bnd)/2
print("="*50)
# Check the result
if abs(f(g) - 0) >= epsilon:
print("Failed on finding the root.")
else:
print("Find an approximated root: {:.04f}".format(g))
# How many steps do we have?
print("# of guesses = {}".format(numGuesses))
Current search region: [0.0000, 10.0000]
Current guess = 5.0000
(lower, current, upper) = (False, True, True)
Current search region: [0.0000, 5.0000]
Current guess = 2.5000
(lower, current, upper) = (False, False, True)
Current search region: [2.5000, 5.0000]
Current guess = 3.7500
(lower, current, upper) = (False, True, True)
Current search region: [2.5000, 3.7500]
Current guess = 3.1250
(lower, current, upper) = (False, True, True)
Current search region: [2.5000, 3.1250]
Current guess = 2.8125
(lower, current, upper) = (False, True, True)
Current search region: [2.5000, 2.8125]
Current guess = 2.6562
(lower, current, upper) = (False, False, True)
==================================================
Find an approximated root: 2.7344
# of guesses = 6
Exercise 3.3#
We have already found a root of equation.
However, our mathematical intuition tells us there are more roots for a quadratic equation. Please find the other root of this equation.
Hint: we had already found a root within \(x \in [0, 10]\) last time. You should try another region.
Now you should realize what is your homework?
Digression: Floating-point numbers#
Something you should know
Try this
x = 0. for i in range(10): x += 0.1 if x == 1.: print(x, "= 1.0") else: print(x, "!= 1.0")
x = 0.
for i in range(10):
x += 0.1
if x == 1.:
print(x, "= 1.0")
else:
print(x, "!= 1.0")
print(2**.5)
0.9999999999999999 != 1.0
1.4142135623730951
Floating-point numbers#
Numbers in decimal system#
Mantissa, exponent, and sign

General form
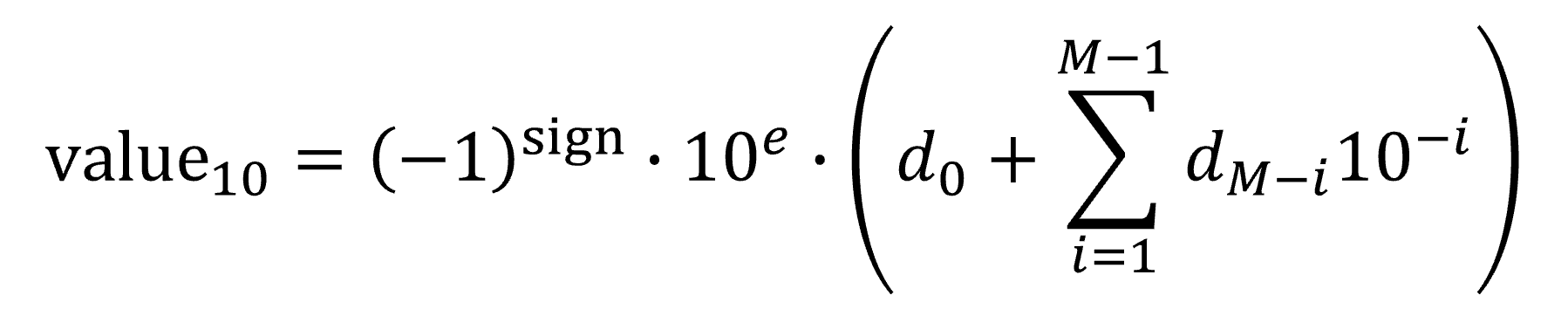
Approximation and precision#
Single-precision floating-point number
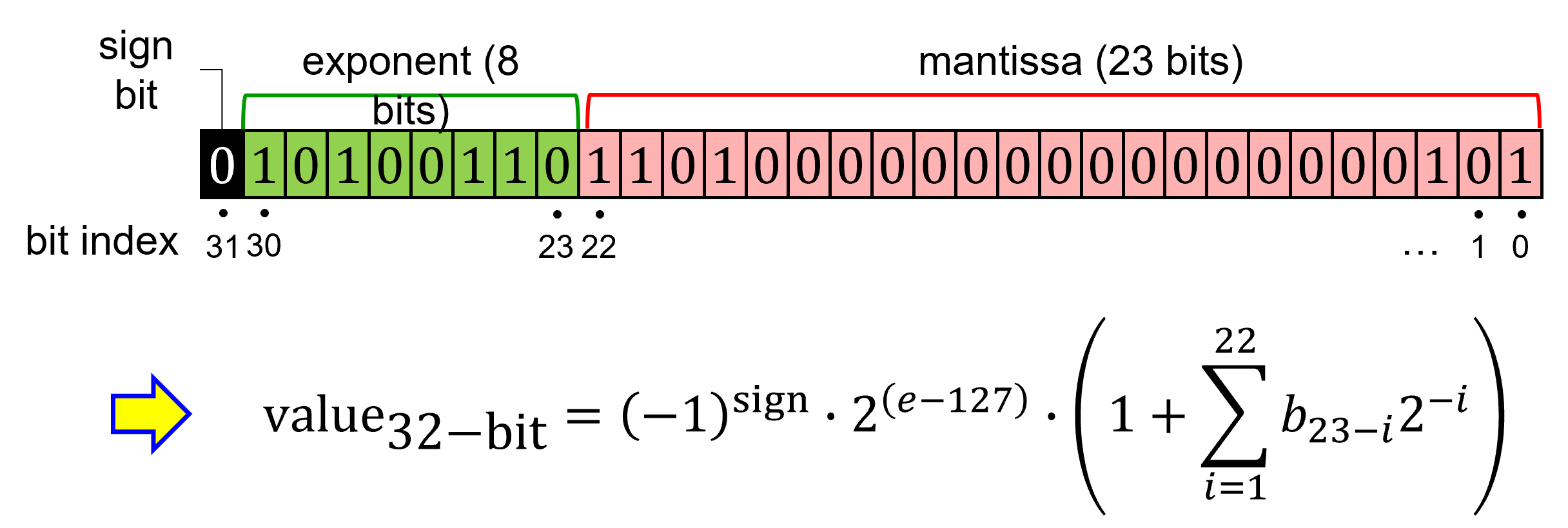
Double-precision floating-point number

Binary numbers: base-2 numbers
\((10100110)_2 = 0 \times 2^0 + 1 \times 2^1 + 1 \times 2^2 + ... + 1 \times 2^5 + ... + 1 \times 2^7 = (166)_{10}\)
\((1.1101)_2 = 1 \times 2^0 + 1 \times 2^{-1} + 1 \times 2^{-2} + 0 \times 2^{-3} + 1 \times 2^{-4} = (1.8125)_{10}\)
General form of floating-point number: \(\pm (1.\text{mantissa}) \times 2^{\text{exponent}}\)
Newton-Raphson method#
A simple and iconic technique for optimization problem (searching the local extreme values)
For example: finding a square root of an arbitrary number \(t\)
It is equivalent to find the solution of this equation: \(f(x) = x^2 - t = 0\)
The solution can be found iteratively via \(x_{n+1} = x_{n} - \frac{f(x_{n})}{f'({x_{n})}} \)
Gradient descent algorithm
# Example of Newton-Raphson method
# Find the square root of an arbitrary number
t = 9487
# Start with a guess
ans = t/2
# Define minimum deviation
epsilon = 0.01
numGuesses = 0
while abs(ans**2 - t) >= epsilon:
numGuesses += 1
ans = ans - (ans**2 - t) / (2*ans)
print("# of guesses: {}".format(numGuesses))
print("{:0.4f} is close enough to the square root of {}.".format(ans, t))
# of guesses: 9
97.4012 is close enough to the square root of 9487.
Find a root of an equation via Newton-Raphson method#
Again, we can numerically solve an equantion via Newton-Raphson method. For example, find a root of this equation:
You just need to follow this procedure:
Start with a guess \(x_n\)
Calculate the error \(E = f(x_n)\).
If the error \(E\) is less than the minimum deviation \(\epsilon\), then we can say we have found an approximated root \(x_n\).
If not, update the guess via \(x_{n+1} = x_{n} - \frac{f(x_{n})}{f'({x_{n})}}\) and repeat step 2 & 3.
# Find the root of an equation via Newton-Raphson method
# Create a function object
f = lambda x: x**2 - 4*x - 5
# Start with a guess
ans = 0
# Define minimum deviation
epsilon = 0.01
numGuesses = 0
while abs(f(ans) - 0) >= epsilon:
numGuesses += 1
ans = ans - (f(ans)) / (2*ans - 2)
print("# of guesses: {}".format(numGuesses))
print("Find an approximated root: {:.04f}".format(ans))
# of guesses: 9
Find an approximated root: -1.0009
Exercise 3.4#
We have already found a root of equation \(x^2 - 4x - 5 = 0\) based on the Newton-Raphson method. However, our mathematical intuition tells us there are more roots for a quadratic equation.
Please try to find the other root of this equation via Newton-Raphson method and explain why we can achieve this.
