06. Recursion and Dictionaries#
Last time#
Tuples
Lists
Mutability and aliasing
Cloning
Today#
Recursion#
The basic idea of recursion is divide and conquer
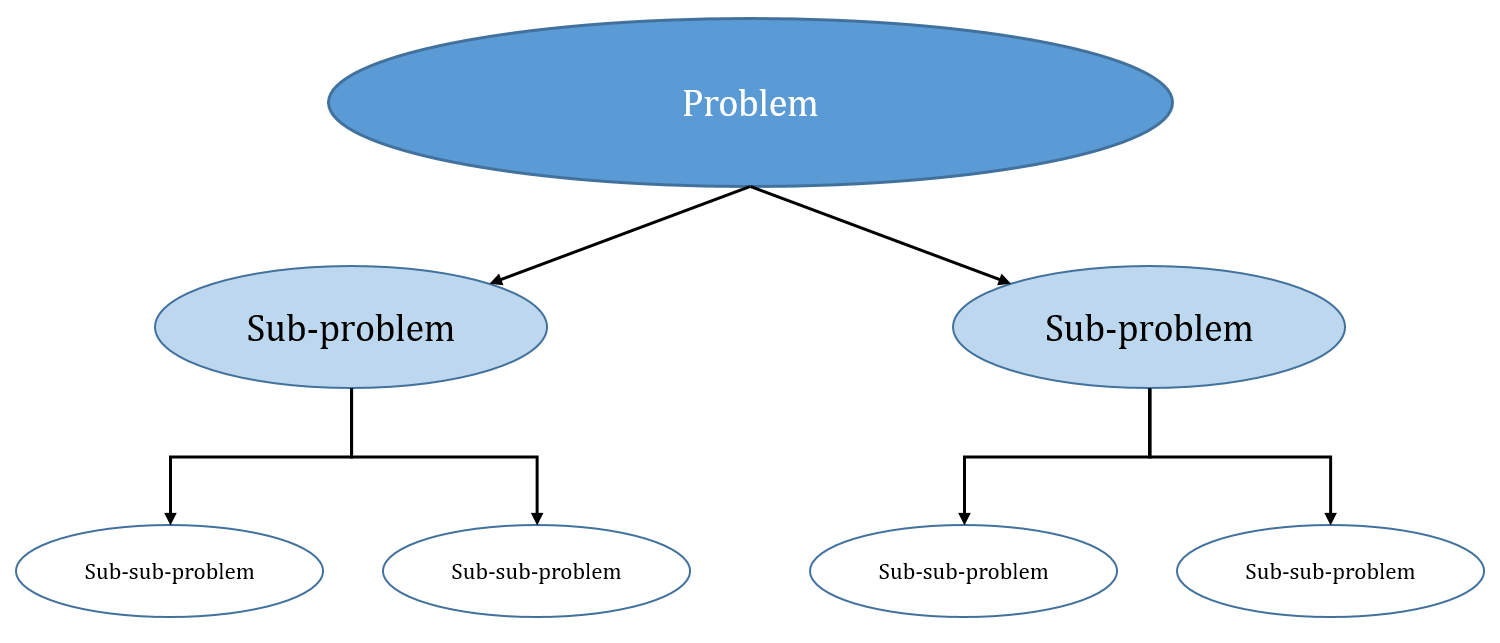
How to implement by programming?
Try to divide the original problem into small versions of the original problem
In practical, write a function that calls itself
Rule of thumb: AVOID CALLING ITSELF INFINITELY
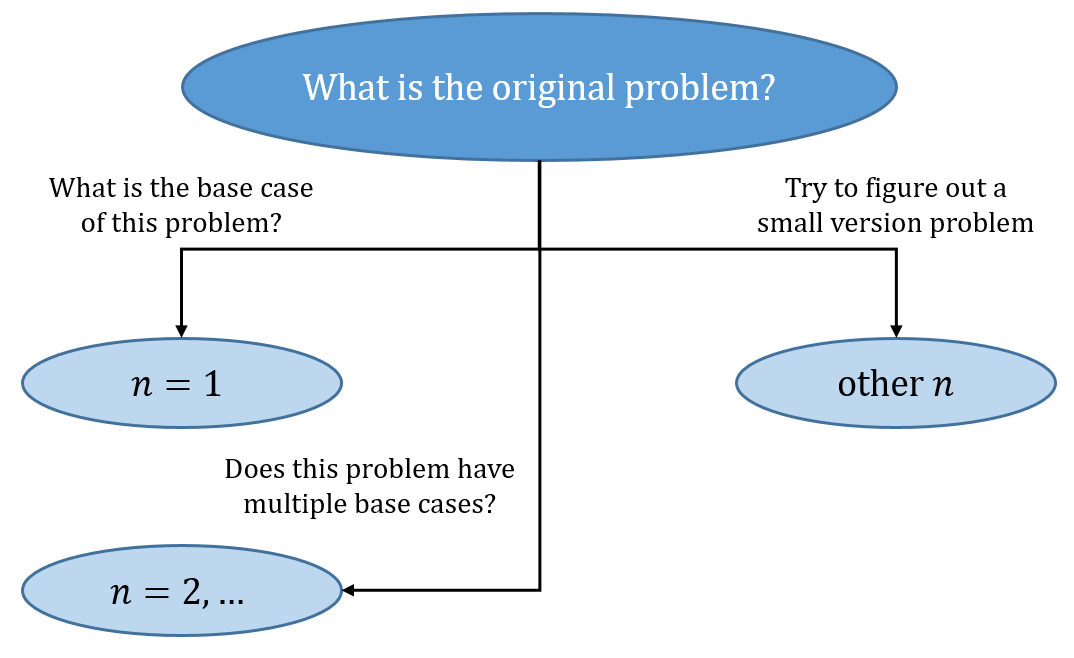
There must be 1 or more base cases in your algorithm
Example I: multiplication#
Multiplication can be regarded as adding itself with designate times
# iterative thinking def multiI(x, a): """ x: multiplicand a: multiplicator """ output = 0 for i in range(a): output += x return output # recursive thinking def multiR(x, a): """ x: multiplicand a: multiplicator """ if a == 1: return x else: return x + multiR(x, a-1)
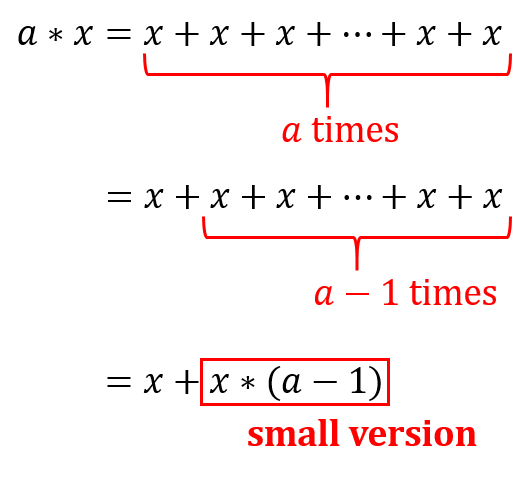
Example II: factorial#
The factorial (denoted or represented as \(n!\)) for a positive number or integer (which is denoted by \(n\)) is the product of all the positive numbers preceding or equivalent to \(n\) (the positive integer).
# iterative thinking def factI(n): """ Return n! """ output = 1 for i in range(n): output *= (i+1) return output # recursive thinking def factR(n): """ Return n! """ if n == 1: return n else: return n * factR(n-1)
Think carefully before you programming#
Exercise 6.1: sum of harmonic series, part II#
Please write a function called
harSumthat aims to return you the sum of a harmonic series \(\displaystyle\sum_{k=1}^{n}\frac{1}{k}\)Please accomplish this task with recursive thinking.
def harSum(n):
"""
Assume that n is a positive integer
Return the sum of n harmonic series
"""
# 自己想
return output
Test your function with different inputs \(n\), for example,
harSum(87).
Exercise 6.2: Fibonacci number#
Please write a function called
fibthat aims to return you the \(n^{th}\) Fibonacci number \(F_n\). The definition of Fibonacci number is:\(F_0 = 0\)
\(F_1 = 1\)
\(F_n = F_{n-1} + F_{n-2}\)
def fib(n):
"""
Assume that n is a positive integer
Return the nth Fibonacci number
"""
# 自己想
return output
Test your function with different inputs \(n\), for example,
fib(10).
Global variable#
Try this
for i in range(10, 40, 5):
print("F({}) is {}.".format(i, fib(i)))
Use global variable to pass the variables inside the scope of a function
def fib(n):
global numFibCalls
numFibCalls += 1
if n == 0:
return 0
elif n == 1:
return 1
else:
return fib(n-1) + fib(n-2)
def testFib(n):
global numFibCalls
for i in range(0, n, 5):
numFibCalls = 0
# Calculate F(n)
print("F({}) is {}.".format(i, fib(i)))
# Summarize how many times that fib was called in this loop
print("# of fib calls = {} times.".format(numFibCalls))
testFib(35)
F(0) is 0.
# of fib calls = 1 times.
F(5) is 5.
# of fib calls = 15 times.
F(10) is 55.
# of fib calls = 177 times.
F(15) is 610.
# of fib calls = 1973 times.
F(20) is 6765.
# of fib calls = 21891 times.
F(25) is 75025.
# of fib calls = 242785 times.
F(30) is 832040.
# of fib calls = 2692537 times.
Dictionaries#
A non-scalar, non-sequenced, and mutable type object
Syntax:
ArbDict = {key1: value1, key2: value2, key3: value3, ...}ArbDict = {1: 123, "1": 456, "Y": "YangMing", "C": "ChiaoTung"}
ArbDict = {1: 123, "1": 456, "Y": "YangMing", "C": "ChiaoTung"}
print(ArbDict[1])
print(ArbDict["1"])
123
456
print(ArbDict[2])
---------------------------------------------------------------------------
KeyError Traceback (most recent call last)
Cell In[3], line 1
----> 1 print(ArbDict[2])
KeyError: 2
print(ArbDict.get(1))
print(ArbDict.get(2))
Add additional key to dict#
ArbDict["NewKey"] = 9876543210
# keys
print(ArbDict.keys())
# values
print(ArbDict.values())
# For more operations... VS code will show you
# Efficient function for Fibonacci number
def fibEff(n, d):
"""
Assume that n is a positive integer
Return the nth Fibonacci number
"""
global numFibEffCalls
numFibEffCalls += 1
if n in d:
return d[n]
else:
ans = fibEff(n-1, d) + fibEff(n-2, d)
d[n] = ans
return ans
d = {0: 0, 1: 1}
numFibEffCalls = 0
print("F({}) is {}.".format(40, fibEff(40, d)))
print("# of FibEff calls = {}".format(numFibEffCalls))
Function with multiple input arguments#
If there are multiple input arguments in a function, you can use
*argsand**kwargsto pass multiple arguments to function.
Parameters |
Description |
|---|---|
|
A tuple of positional arguments values. |
|
A dict of keyword arguments values. |
# Example for *args
def test_func1(numList, *args):
for item in numList:
print(item)
print("args:", args)
for item in args:
print(item)
a = [9, 4, 8, 7]
b = [8, 9, 6, 4]
c = ["习近平小熊维尼", "黨說不缺水不缺電不缺蛋不缺工不缺疫苗"]
d = ["OO地區沒有勞基法", "黨說沒有討論沒有民主"]
test_func1(a)
test_func1(a, b)
test_func1(a, b, c, d)
# Example for **kwargs
def test_func2(numList, **kwargs):
for item in numList:
print(item)
print("kwargs:", kwargs)
for key in kwargs.keys():
print(kwargs[key])
a = [9, 4, 8, 7]
b = [8, 9, 6, 4]
c = ["习近平小熊维尼", "黨說不缺水不缺電不缺蛋不缺工不缺疫苗"]
d = ["OO地區沒有勞基法"]
test_func2(
a,
item1=b,
item2=c,
item3=d,
)
# Using *args and **kwargs in the same time
def test_func3(numList, *args, **kwargs):
for item in numList:
print(item)
print("args:", args)
for item in args:
print(item)
print("kwargs:", kwargs)
for key in kwargs.keys():
print(kwargs[key])
test_func3(
a,
b,
item1=c,
item2=d,
)
Exercise 6.3: sum of geometric series#
Please write a function called
geoSumthat aims to return you the sum of a harmonic series \(\displaystyle\sum_{k=1}^{n}\frac{1}{2^k}\)
def geoSum(n):
"""
Assume that n is a positive integer
Return the sum of n geometric series
"""
# 自己想
return output
Test your function with different inputs \(n\), for example,
geoSum(87).
