10. Introduction to Computational Complexity

10. Introduction to Computational Complexity#

Last time#

  • Inheritance

  • Decorator

Today#

How to evaluate the efficiency of your algorithm?#

Why do we need this?#

  1. In Nov. 2016, Google reported that there were \(130\) trillion pages in their database, covering more than \(100,000 TB\).

  2. Today, Google processes over \(100k\) searches every single second (Internet Live States).


  3. Think of this, how long does “Google search” search for the keywords among these pages?

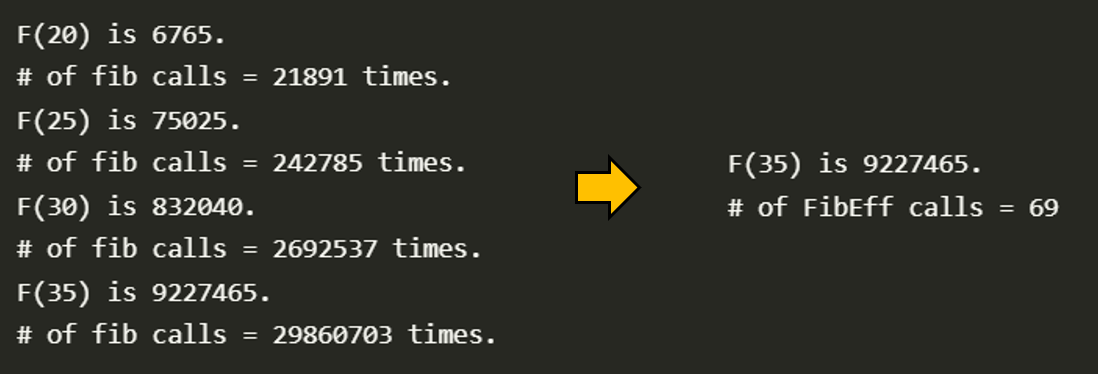
  4. In 2022, we had introduced some efficient ways to calculate the Fibonacci series so that we did not need too much steps for the answer.


How to evaluate the efficiency of programs?#

  1. Measure with a timer

  2. Count the operations

  3. Abstract notion of orders of growth

Measure with a timer#

  • Use time module

import time

def testFunc(n=100):
    for i in range(n):
        time.sleep(1e-3)


# Test 1
t0 = time.time()            # Start time
testFunc()
t1 = time.time() - t0       # End time

print("Execution time of test 1: {:04f} sec".format(t1))

Execution time of test 1: 0.120357 sec

  • Consistency of timer

# Test 2

n = 10
tList = []

for i in range(n):
    t0 = time.time()            # Start time
    testFunc()
    t1 = time.time() - t0       # End time
    
    tList.append(t1)

    print("Execution time of {}: {:04f} sec".format(i+1, t1))

print("Average execution time: {:04f} sec".format(sum(tList)/n))

Execution time of 1: 0.124133 sec

Execution time of 2: 0.117344 sec

Execution time of 3: 0.114974 sec

Execution time of 4: 0.114514 sec

Execution time of 5: 0.116009 sec

Execution time of 6: 0.160542 sec

Execution time of 7: 0.138660 sec

Execution time of 8: 0.115893 sec

Execution time of 9: 0.115478 sec

Execution time of 10: 0.116419 sec
Average execution time: 0.123396 sec

Count of the operations#

  • Assume every steps take a constant time


Brief summary#

Timer

Count

Depends on algorithms

o

o

Depends on implementations

x

x

Depends on computers

o

x

Which operations should it count?

x

x

  • However, the algorithms are usually dependent on the value of input data.

  • We want to evaluate the complexity and the scalability of algorithms in terms of the size of input data.

Orders of growth and \(O\) notation#

  • Evaluate the efficiency of program when input is very big.

  • Express the growth of program’s run time as input size grows.

  • Only consider the worst case.

  • Use asymptotic notation, do not provide an exact growth.

  • Only focus on the dominant section of program.

A simple example#

  • Consider a linear search algorithm:

def search(L, e):
    for x in L:
        if x == e:
            return True
    return False

  • Possible situations:

    1. Best case:

      • The first element is the target.

    2. Average case:

      • The target element is located around the middle of the list.

    3. Worst case:

      • The target element is located in the end of the list, or not in the list.

  • In this case, the order of growth is \(n\).

Asymptotic notation#

def f(x):
   ans = 0
   for i in range(1000):
       ans += 1
   print("Number of additions so far: {}".format(ans))

  • The order of growth is \(O(1000)\), independent to the input \(x\).

def f(x):
    ans = 0
    for i in range(x):
        ans += 1
    print("Number of additions so far: {}".format(ans))

  • The order of growth is \(O(x)\), linearly dependent to the input \(x\).

def f(x):
    ans = 0
    for i in range(x):
        for j in range(x):
            ans += 1
    print("Number of additions so far: {}".format(ans))

  • The order of growth is \(O(x^2)\).

def f(x):
    ans = 0

    for i in range(1000):
        ans += 1
    print("Number of additions so far: {}".format(ans))

    for i in range(x):
        ans += 1
    print("Number of additions so far: {}".format(ans))

    for i in range(x):
        for j in range(x):
            ans += 1
    print("Number of additions so far: {}".format(ans))

  • The order of growth is still \(O(x^2)\).

This time, details do not matter#

\(O()\)

Class

\(n^2 + n + 1000\)

\(O(n^2)\)

quadratic

\(3n^2 + n + 1000\)

\(O(n^2)\)

quadratic

\(0.01n^2 + 100000n + 2^{9487}\)

\(O(n^2)\)

quadratic

\(\log{n} + 100000n + 3\)

\(O(n)\)

linear

\(64 \cdot n \cdot \log{n} + 26n + 111\)

\(O(n \log{n})\)

log-linear

\(n^{1024} + 26^{n} + 810502\)

\(O(26^{n})\)

exponential

Searching algorithms#

  • Searching an element in a sorted list

3. Bisection search#

def searchBi(L, target):
    def search(L, target, low, high):
        if high == low:
            return (L[low]==target)
        
        mid = (low + high)//2

        if L[mid] == target:
            return True
        
        elif L[mid] > target:
            if low == mid:
                return False
            else:
                return search(L, target, low, mid-1)
        
        else:
            return search(L, target, mid+1, high)
    
    if len(L) == 0:
        return False
    else:
        return search(L, target, 0, len(L)-1)

  • What is the computational complexity of this algorithm?

Contents